1. Lenguajes Formales
2. Autómatas Finitos
3. Regularidad de Lenguajes
Operaciones sobre Palabras
Una palabra, frase o cadena se define como una secuencia finita y ordenada de símbolos pertenecientes a un alfabeto. Es importante mencionar la existencia de la palabra vacía (λ), la cual consiste en una cadena de longitud cero. Como explicamos anteriormente, esta palabra vacía equivale a un String vacío.
En el ámbito de las operaciones sobre palabras, se sigue un criterio diferente en comparación con las operaciones numéricas. Por ejemplo, el proceso de elevar un número al cuadrado es distinto al de elevar una cadena de caracteres. Por lo tanto, es necesario definir claramente las acciones a realizar en cada operación, dado que estas operaciones son ampliamente utilizadas en la actualidad, especialmente en el contexto de los lenguajes de programación.
A continuación, exploraremos las principales operaciones sobre palabras en el campo de los lenguajes formales.
Concatenación
La concatenación de dos palabras se representa con un punto (·) y se define de la siguiente manera:
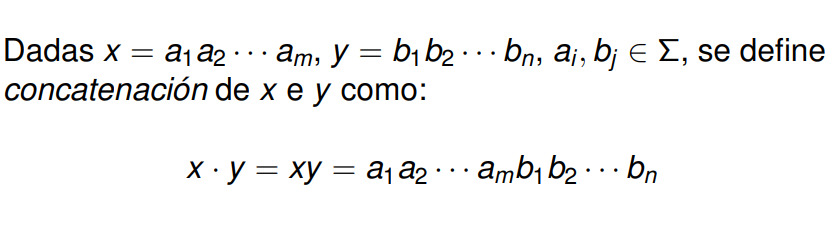
Es decir, que dadas dos palabras x e y, x · y da como resultado una nueva palabra compuesta por todos los símbolos de la palabra x seguidos por todos los símbolos de la palabra y.
Por ejemplo, digamos que x = «monta» e y = «puercos», si realizamos la operación x·y obtendremos la palabra
«montapuercos».
monta · puercos = montapuercos
Por esta razón recibe el nombre de concatenación, porque el propósito de esta operación es concatenar una palabra
con otra u otras.
La concatenación es especialmente útil en el campo de la programación,. Por ejemplo, si un usuario llamado «Ana»
inicia sesión, podríamos concatenar su nombre con un mensaje de saludo para que se muestre como
«¡Hola, Ana! ¡Bienvenido de nuevo!». Aquí, la concatenación nos permite combinar dinámicamente el nombre del
usuario con el mensaje de saludo estático para crear un mensaje personalizado que se adapte a cada usuario que
inicia sesión.
Propiedades de la concatenación
Sean x, y, z ∈ Σ* y a ∈ Σ
La concatenación cumple las siguiente propiedades:
1 – Asociativa: (x · y) · z = x · (y · z)
2 – Existencia de elemento neutro (λ): xλ = λx = x
Dado que λ, la cadena vacía, no contiene ningún caracter, podemos concatenarla con cualquier otra palabra x
y no producirá ningún cambio, es decir, el resultado será la propia palabra x.
3 – |xy| = |x| + |y|
Esta propiedad resulta bastante lógica, y es que, si concatenamos dos palabras x, compuesta por n simbolos, e y, compuesta por m simbolos, el resultado de la operación (la palabra xy) poseerá una longitud de n+m símbolos. Por ejemplo, sea x = «000» e y = «111», ambas de longitud 3. El resultado de x·y será «000111» y su longitud la suma de las dos palabras que la componen (3 + 3 = 6).
Potencia
Considerando la concatenación, se define potencia de una palabra como:
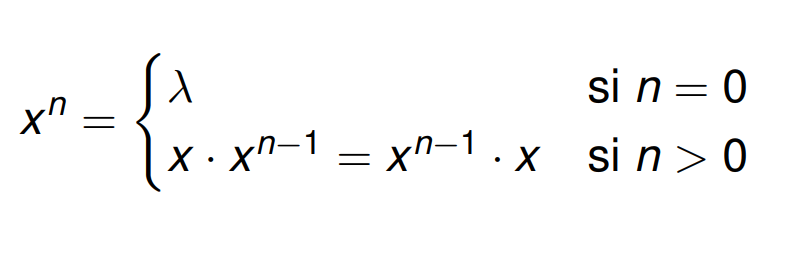
Esta fórmula recursiva se interpreta de la siguiente manera:
λ si n = 0 -> Toda palabra elevada a cero da como resultado la cadena vacía, λ.
x · x^(n−1) = x^(n−1)· x si n > 0 -> Una palabra x elevada a un entero n, es el resultado de concatenar esta misma palabra x consigo misma n veces.
Por ejemplo, sea la palabra x = «010», entonces x^4 = «010010010010» y x^0 = λ.
Prefijos, Sufijos y Segmentos
Dados x y t, palabras de Σ*, t es un segmento de x si existen u y v tales que x = u · t · v.
Si u = λ, entonces t es un prefijo de x.
Si v = λ, entonces t es un sufijo de x.
Veamos esto con un ejemplo, para ello trabajaremos con la palabra «1010» sobre el alfabeto binario.
Prefijos
Para obtener el conjunto de prefijos de una palabra simplemente tenemos que empezar desde la posición cero e ir construyendo palabras con los símbolos posteriores. Con nuestra palabra de ejemplo «1010», podemos conseguir Prefijos(1010) = {λ, 1,10,101 y 1010}, como resultado de colocarnos en la posición cero e ir desplazándonos 0, 1, 2, y 3 posiciones respectivamente.
Sufijos
Para obtener el conjunto de sufijos de una palabra simplemente tenemos que situarnos detrás del último símbolo de esta e ir construyendo palabras con los símbolos anteriores. Con nuestra palabra de ejemplo «1010», tenemos que Sufijos(1010) = {λ, 0, 10, 010 y 1010}, como resultado de colocarnos en la última posición e ir desplazándonos 0, 1, 2, y 3 posiciones respectivamente.
Segmentos
Los segmentos de una palabra x son, básicamente, todas aquellas palabras que podemos formar tomando caracteres de x respetando el orden en el que aparecen en esta desde todas sus posiciones. Con nuestra palabra de ejemplo «1010», podemos conseguir Segementos(1010) = {λ, 0, 1, 01,10, 010, 101 y 1010}. Es fácil percatarse de que los conjuntos de prefijos y sufijos de una palabra x están contenidos obligatoriamente en sus segmentos.
Reverso
Dados x, y ∈ Σ* y un símbolo a del alfabeto, se define el reverso de una palabra como:
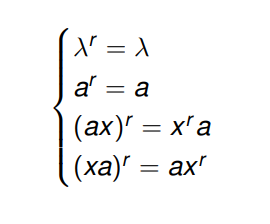
Es decir, tenemos dos casos base:
λ^r = λ -> El reverso de la cadena vacía es la propia cadena vacía
a^r = a -> El reverso de un único símbolo es este mismo símbolo
Y dos casos generales:
(ax)^r = x^ra
(xa)^r = ax^r -> El reverso de una palabra x compuesta por más de un símbolo es el resultado de ir aplicando recursivamente el reverso a cada uno de sus símbolos.
Para entendernos, el reverso de una palabra es esta misma palabra en orden inverso, por ejemplo, sea la palabra X = «web», entonces X^r = «bew».
Propiedades del reverso
1 (x^r)^r = x
2 (xy)^r = y^r ·x^r
3 (x^n)^r = (x^r)^n para cualquier entero n ≥ 0
1. Lenguajes Formales
2. Autómatas Finitos
3. Regularidad de Lenguajes
Operaciones sobre Palabras
Una palabra, frase o cadena se define como una secuencia finita y ordenada de símbolos pertenecientes a un alfabeto. Es importante mencionar la existencia de la palabra vacía (λ), la cual consiste en una cadena de longitud cero. Como explicamos anteriormente, esta palabra vacía equivale a un String vacío.
En el ámbito de las operaciones sobre palabras, se sigue un criterio diferente en comparación con las operaciones numéricas. Por ejemplo, el proceso de elevar un número al cuadrado es distinto al de elevar una cadena de caracteres. Por lo tanto, es necesario definir claramente las acciones a realizar en cada operación, dado que estas operaciones son ampliamente utilizadas en la actualidad, especialmente en el contexto de los lenguajes de programación.
A continuación, exploraremos las principales operaciones sobre palabras en el campo de los lenguajes formales.
Concatenación
La concatenación de dos palabras se representa con un punto (·) y se define de la siguiente manera:
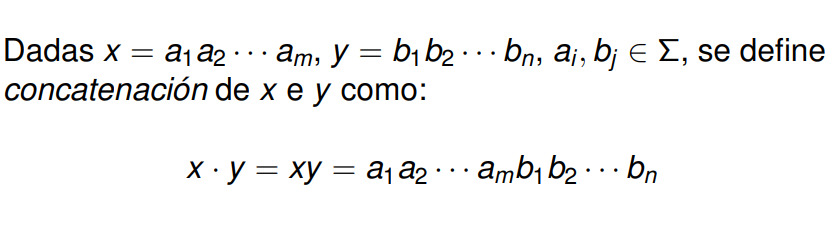
Es decir, que dadas dos palabras x e y, x · y da como resultado una nueva palabra compuesta por todos los símbolos de la palabra x seguidos por todos los símbolos de la palabra y.
Por ejemplo, digamos que x = «monta» e y = «puercos», si realizamos la operación x·y obtendremos la palabra
«montapuercos».
monta · puercos = montapuercos
Por esta razón recibe el nombre de concatenación, porque el propósito de esta operación es concatenar una palabra
con otra u otras.
La concatenación es especialmente útil en el campo de la programación,. Por ejemplo, si un usuario llamado «Ana»
inicia sesión, podríamos concatenar su nombre con un mensaje de saludo para que se muestre como
«¡Hola, Ana! ¡Bienvenido de nuevo!». Aquí, la concatenación nos permite combinar dinámicamente el nombre del
usuario con el mensaje de saludo estático para crear un mensaje personalizado que se adapte a cada usuario que
inicia sesión.
Propiedades de la concatenación
Sean x, y, z ∈ Σ* y a ∈ Σ
La concatenación cumple las siguiente propiedades:
1 – Asociativa: (x · y) · z = x · (y · z)
2 – Existencia de elemento neutro (λ): xλ = λx = x
Dado que λ, la cadena vacía, no contiene ningún caracter, podemos concatenarla con cualquier otra palabra x
y no producirá ningún cambio, es decir, el resultado será la propia palabra x.
3 – |xy| = |x| + |y|
Esta propiedad resulta bastante lógica, y es que, si concatenamos dos palabras x, compuesta por n simbolos, e y, compuesta por m simbolos, el resultado de la operación (la palabra xy) poseerá una longitud de n+m símbolos. Por ejemplo, sea x = «000» e y = «111», ambas de longitud 3. El resultado de x·y será «000111» y su longitud la suma de las dos palabras que la componen (3 + 3 = 6).
Potencia
Considerando la concatenación, se define potencia de una palabra como:
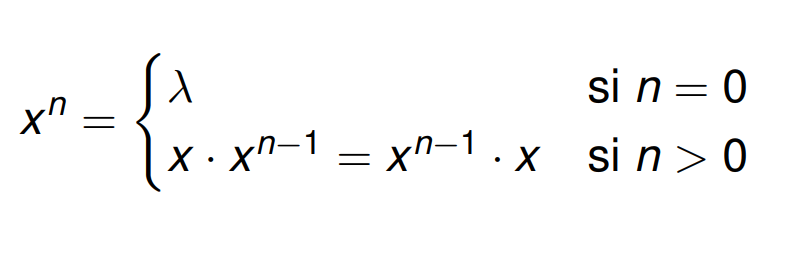
Esta fórmula recursiva se interpreta de la siguiente manera:
λ si n = 0 -> Toda palabra elevada a cero da como resultado la cadena vacía, λ.
x · x^(n−1) = x^(n−1)· x si n > 0 -> Una palabra x elevada a un entero n, es el resultado de concatenar esta misma palabra x consigo misma n veces.
Por ejemplo, sea la palabra x = «010», entonces x^4 = «010010010010» y x^0 = λ.
Prefijos, Sufijos y Segmentos
Dados x y t, palabras de Σ*, t es un segmento de x si existen u y v tales que x = u · t · v.
Si u = λ, entonces t es un prefijo de x.
Si v = λ, entonces t es un sufijo de x.
Veamos esto con un ejemplo, para ello trabajaremos con la palabra «1010» sobre el alfabeto binario.
Prefijos
Para obtener el conjunto de prefijos de una palabra simplemente tenemos que empezar desde la posición cero e ir construyendo palabras con los símbolos posteriores. Con nuestra palabra de ejemplo «1010», podemos conseguir Prefijos(1010) = {λ, 1,10,101 y 1010}, como resultado de colocarnos en la posición cero e ir desplazándonos 0, 1, 2, y 3 posiciones respectivamente.
Sufijos
Para obtener el conjunto de sufijos de una palabra simplemente tenemos que situarnos detrás del último símbolo de esta e ir construyendo palabras con los símbolos anteriores. Con nuestra palabra de ejemplo «1010», tenemos que Sufijos(1010) = {λ, 0, 10, 010 y 1010}, como resultado de colocarnos en la última posición e ir desplazándonos 0, 1, 2, y 3 posiciones respectivamente.
Segmentos
Los segmentos de una palabra x son, básicamente, todas aquellas palabras que podemos formar tomando caracteres de x respetando el orden en el que aparecen en esta desde todas sus posiciones. Con nuestra palabra de ejemplo «1010», podemos conseguir Segementos(1010) = {λ, 0, 1, 01,10, 010, 101 y 1010}. Es fácil percatarse de que los conjuntos de prefijos y sufijos de una palabra x están contenidos obligatoriamente en sus segmentos.
Reverso
Dados x, y ∈ Σ* y un símbolo a del alfabeto, se define el reverso de una palabra como:
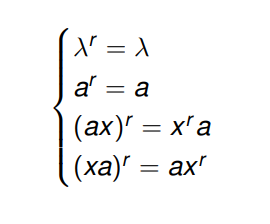
Es decir, tenemos dos casos base:
λ^r = λ -> El reverso de la cadena vacía es la propia cadena vacía
a^r = a -> El reverso de un único símbolo es este mismo símbolo
Y dos casos generales:
(ax)^r = x^ra
(xa)^r = ax^r -> El reverso de una palabra x compuesta por más de un símbolo es el resultado de ir aplicando recursivamente el reverso a cada uno de sus símbolos.
Para entendernos, el reverso de una palabra es esta misma palabra en orden inverso, por ejemplo, sea la palabra X = «web», entonces X^r = «bew».
Propiedades del reverso
1 (x^r)^r = x
2 (xy)^r = y^r ·x^r
3 (x^n)^r = (x^r)^n para cualquier entero n ≥ 0
1. Lenguajes Formales
2. Autómatas Finitos
3. Regularidad de Lenguajes
Operaciones sobre Palabras
Una palabra, frase o cadena se define como una secuencia finita y ordenada de símbolos pertenecientes a un alfabeto. Es importante mencionar la existencia de la palabra vacía (λ), la cual consiste en una cadena de longitud cero. Como explicamos anteriormente, esta palabra vacía equivale a un String vacío.
En el ámbito de las operaciones sobre palabras, se sigue un criterio diferente en comparación con las operaciones numéricas. Por ejemplo, el proceso de elevar un número al cuadrado es distinto al de elevar una cadena de caracteres. Por lo tanto, es necesario definir claramente las acciones a realizar en cada operación, dado que estas operaciones son ampliamente utilizadas en la actualidad, especialmente en el contexto de los lenguajes de programación.
A continuación, exploraremos las principales operaciones sobre palabras en el campo de los lenguajes formales.
Concatenación
La concatenación de dos palabras se representa con un punto (·) y se define de la siguiente manera:
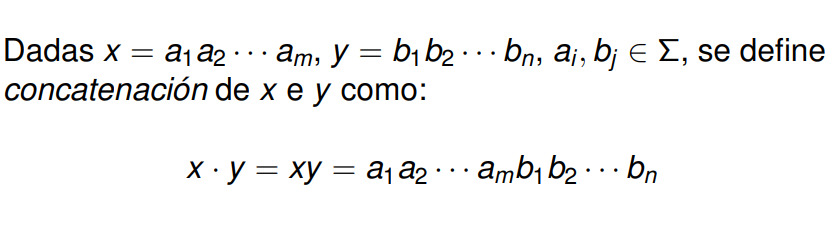
Es decir, que dadas dos palabras x e y, x · y da como resultado una nueva palabra compuesta por todos los símbolos de la palabra x seguidos por todos los símbolos de la palabra y.
Por ejemplo, digamos que x = «monta» e y = «puercos», si realizamos la operación x·y obtendremos la palabra
«montapuercos».
monta · puercos = montapuercos
Por esta razón recibe el nombre de concatenación, porque el propósito de esta operación es concatenar una palabra
con otra u otras.
La concatenación es especialmente útil en el campo de la programación,. Por ejemplo, si un usuario llamado «Ana»
inicia sesión, podríamos concatenar su nombre con un mensaje de saludo para que se muestre como
«¡Hola, Ana! ¡Bienvenido de nuevo!». Aquí, la concatenación nos permite combinar dinámicamente el nombre del
usuario con el mensaje de saludo estático para crear un mensaje personalizado que se adapte a cada usuario que
inicia sesión.
Propiedades de la concatenación
Sean x, y, z ∈ Σ* y a ∈ Σ
La concatenación cumple las siguiente propiedades:
1 – Asociativa: (x · y) · z = x · (y · z)
2 – Existencia de elemento neutro (λ): xλ = λx = x
Dado que λ, la cadena vacía, no contiene ningún caracter, podemos concatenarla con cualquier otra palabra x
y no producirá ningún cambio, es decir, el resultado será la propia palabra x.
3 – |xy| = |x| + |y|
Esta propiedad resulta bastante lógica, y es que, si concatenamos dos palabras x, compuesta por n simbolos, e y, compuesta por m simbolos, el resultado de la operación (la palabra xy) poseerá una longitud de n+m símbolos. Por ejemplo, sea x = «000» e y = «111», ambas de longitud 3. El resultado de x·y será «000111» y su longitud la suma de las dos palabras que la componen (3 + 3 = 6).
Potencia
Considerando la concatenación, se define potencia de una palabra como:
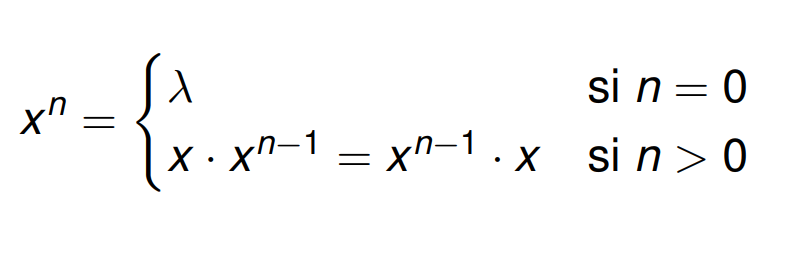
Esta fórmula recursiva se interpreta de la siguiente manera:
λ si n = 0 -> Toda palabra elevada a cero da como resultado la cadena vacía, λ.
x · x^(n−1) = x^(n−1)· x si n > 0 -> Una palabra x elevada a un entero n, es el resultado de concatenar esta misma palabra x consigo misma n veces.
Por ejemplo, sea la palabra x = «010», entonces x^4 = «010010010010» y x^0 = λ.
Prefijos, Sufijos y Segmentos
Dados x y t, palabras de Σ*, t es un segmento de x si existen u y v tales que x = u · t · v.
Si u = λ, entonces t es un prefijo de x.
Si v = λ, entonces t es un sufijo de x.
Veamos esto con un ejemplo, para ello trabajaremos con la palabra «1010» sobre el alfabeto binario.
Prefijos
Para obtener el conjunto de prefijos de una palabra simplemente tenemos que empezar desde la posición cero e ir construyendo palabras con los símbolos posteriores. Con nuestra palabra de ejemplo «1010», podemos conseguir Prefijos(1010) = {λ, 1,10,101 y 1010}, como resultado de colocarnos en la posición cero e ir desplazándonos 0, 1, 2, y 3 posiciones respectivamente.
Sufijos
Para obtener el conjunto de sufijos de una palabra simplemente tenemos que situarnos detrás del último símbolo de esta e ir construyendo palabras con los símbolos anteriores. Con nuestra palabra de ejemplo «1010», tenemos que Sufijos(1010) = {λ, 0, 10, 010 y 1010}, como resultado de colocarnos en la última posición e ir desplazándonos 0, 1, 2, y 3 posiciones respectivamente.
Segmentos
Los segmentos de una palabra x son, básicamente, todas aquellas palabras que podemos formar tomando caracteres de x respetando el orden en el que aparecen en esta desde todas sus posiciones. Con nuestra palabra de ejemplo «1010», podemos conseguir Segementos(1010) = {λ, 0, 1, 01,10, 010, 101 y 1010}. Es fácil percatarse de que los conjuntos de prefijos y sufijos de una palabra x están contenidos obligatoriamente en sus segmentos.
Reverso
Dados x, y ∈ Σ* y un símbolo a del alfabeto, se define el reverso de una palabra como:
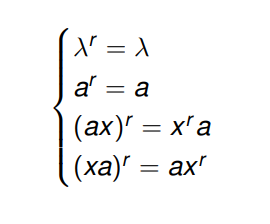
Es decir, tenemos dos casos base:
λ^r = λ -> El reverso de la cadena vacía es la propia cadena vacía
a^r = a -> El reverso de un único símbolo es este mismo símbolo
Y dos casos generales:
(ax)^r = x^ra
(xa)^r = ax^r -> El reverso de una palabra x compuesta por más de un símbolo es el resultado de ir aplicando recursivamente el reverso a cada uno de sus símbolos.
Para entendernos, el reverso de una palabra es esta misma palabra en orden inverso, por ejemplo, sea la palabra X = «web», entonces X^r = «bew».
Propiedades del reverso
1 (x^r)^r = x
2 (xy)^r = y^r ·x^r
3 (x^n)^r = (x^r)^n para cualquier entero n ≥ 0
