1. Lenguajes Formales
2. Autómatas Finitos
3. Regularidad de Lenguajes
Operaciones sobre Lenguajes
Una vez que hemos comprendido los conceptos de símbolo, alfabeto y palabra, y hemos explorado las operaciones que podemos realizar sobre estas últimas, es momento de introducir el concepto de lenguaje y las operaciones relacionadas con ellos.
A continuación, nos adentraremos en algunas de las operaciones principales sobre lenguajes dentro del campo de los lenguajes formales.
Definición de lenguaje
Un lenguaje L es un subconjunto de Σ* (la clausura de Kleene sobre un determinado alfabeto Sigma). Se incluyen:
∅ (lenguaje vacío, no contiene ninguna palabra)
Σ*(todas las palabras posibles sobre Σ)
Es importante matizar que los lenguajes son conjuntos de palabras sobre un determinado alfabeto. La naturaleza de conjunto de los lenguajes implica que se rigen por las propiedades de la Teoría de Conjuntos, tanto en notación como en las operaciones aplicables sobre ellos.
En la Teoría de Autómatas, los lenguajes juegan un papel fundamental, ya que los autómatas, como veremos en los próximos temas, son máquinas abstractas diseñadas para procesar entradas. Por lo tanto, al analizar un lenguaje dado, podemos determinar si es computable o no por un autómata.
Además, los lenguajes tienen una serie de propiedades que iremos desarrollando a lo largo de este curso. Por el momento solo nos concierne saber que estos pueden ser:
Finito: si tiene un número finito de palabras
Infinito numerable: podemos representarlo, pero contiene un número infinito de palabras
Notación de lenguajes
Dado que los lenguajes son conjuntos, la notación de estos mismos es muy similar. Para referirnos a un lenguaje
podemos hacerlo de dos formas. Digamos que Σ = {0,1} y Li una serie de lenguajes contenidos en Σ*.
Por extensión
Un conjunto se determina por extensión cuando se listan explícitamente los elementos del conjunto. Lógicamente, solo podremos referirnos a un lenguaje finito por extensión.
L1 = {λ,0,1,00,01,10,11} -> Lenguaje que contiene todas las palabras en Σ de longitud menor o igual a 2.
L2 = {000,001,010,011,100,101,110,111} -> Lenguaje que contiene todas las palabras de longitud 3 en Σ.
Por comprensión
Un conjunto se determina por comprensión, cuando se da una propiedad que cumplen todos los elementos del conjunto.
L1 = {x ∈ {0,1}* : |x| <= 2 } -> De esta forma citamos que L1 contiene todas las palabras x en la Clausura de Kleene sobre el alfabeto binario tal que su longitud es menor o igual a 2.
L2 = {x ∈ {0,1}* : |x| = 3 } -> Palabras de longitud 3.
L3 = {x ∈ {0,1}* : |x|0 MOD 2 = 0 } -> En este caso estamos inidcando que L3 contiene todas las palabras x en la Clausura de Kleene sobre el alfabeto binario tal que el número de ceros contenido en dichas palabras es par.
Es importante destacar que, a diferencia de los anteriores dos lenguajes L1 y L2, este lenguaje es infinito. Sin embargo, podemos especificar las propiedades que cumplen todas sus palabras. Así pues, dada una palabra cualquiera construida con ceros y/o unos seremos capaces de determinar si esta pertenece o no a L3.
Si tienes problemas para entender estos conceptos, en el siguiente vídeo tratamos las operaciones con conjuntos y su notación.
Una vez desarrollada la definición de lenguaje, veamos qué operaciones podemos realizar sobre estos.
Operaciones Booleanas
Como ya hemos explicado, los lenguajes son conjuntos formados por palabras. Esto significa que podemos realizar sobre ellos las operaciones booleanas definidas en conjuntos.
Unión
L1 U L2 = {x ∈ Σ∗: x ∈ L1 ∨ x ∈ L2} -> La unión de dos lenguajes da como resultado un nuevo lenguaje que contiene todas las palabras de cada uno de estos, comunes y no comunes (sin repetir). Por ejemplo:
L1 = {λ,0,1,00,01,10,11}
L2 = {000,001,010,011,100,101,110,111}
L1 U L2 = {λ,0,1,00,01,10,11,000,001,010,011,100,101,110,111}
Intersección:
L1 ∩ L2 = {x ∈ Σ* : x ∈ L1 ∧ x ∈ L2} -> La intersección de dos lenguajes da como resultado un nuevo lenguaje que contiene únicamente las palabras presentes en ambos, comunes (sin repetir). Por ejemplo:
L1 = {λ,0,1,00,01,10,11}
L2 = {000,001,010,011,100,101,110,111}
L1 U L2 = ∅ -> En este caso, al no tener palabras en común L1 y L2, su intersección da como resultado el conjunto vacío.
Propiedades Unión e Intersección
1.Asociativa
2.Conmutativa
3.Elemento neutro
- Unión: ∅ -> La unión de un lenguaje L con ∅ (el conjunto vacío) da como resultado el propio lenguaje L
- Intersección: Σ* -> La intersección de un lenguaje L con Σ* (todas las palabras posibles sobre un determinado alfabeto) da como resultado el propio lenguaje L.
4.Distributivas:
- L1 ∪ (L2 ∩ L3) = (L1 ∪ L2) ∩ (L1 ∪ L3)
- L1 ∩ (L2 ∪ L3) = (L1 ∩ L2) ∪ (L1 ∩ L3)
Complementación
Usualmente se representa con una línea en la parte superior del lenguaje, tal que así:

Sin embargo, también podemos encontrarla como una C en forma de exponente L^C -> complementario de C.
L^C = {x ∈ Σ*: x ∉ L} -> La complementación o complementario de un lenguaje L definido sobre un determinado alfabeto da como resultado un lenguaje que contiene todas las palabras que se pueden formar sobre dicho alfabeto y no se encuentran contenidas en L.
L1 = {x ∈ {0,1}* : |x| <= 2 }
L1^C = {x ∈ {0,1}* : |x| > 2 } -> El complementario de L1 es un lenguaje que contiene todas las palabras de longitud
mayor que dos.
Propiedades Complementación
1. Σ* = ∅
Por definición, la Clausura de Kleene recoge todas las palabras posibles sobre un alfabeto, de modo que su complementario no contiene ninguna palabra.
2. ∅^C = Σ*
3. (L^C)^C = L -> Si aplicamos dos veces la complementación a un lenguaje L, obtenemos el propio lenguaje L.
Operaciones definidas a partir de las booleanas
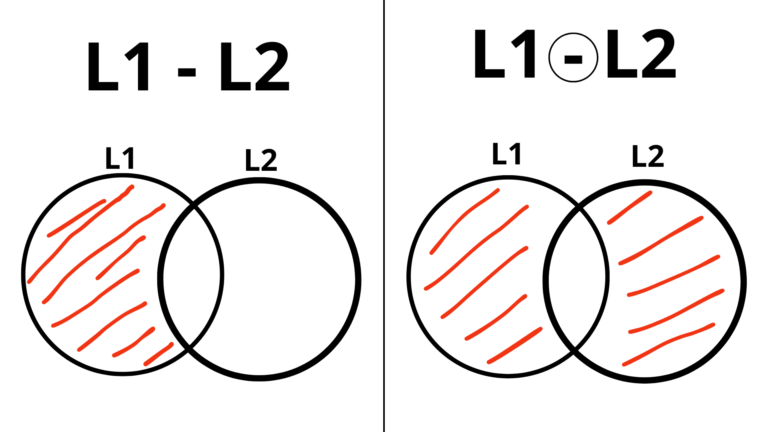
- Diferencia: L1 − L2 = L1 ∩ L2^C -> Palabras contenidas en L1 y no contenidas en L2
- Diferencia simétrica: L1 ⊖ L2 = (L1 ∩ L2^C) U (L1^C ∩ L2) -> Unión de palabras no comunes
Operaciones racionales: Producto
L1 · L2 = {xy ∈ Σ*: x ∈ L1 ∧ y ∈ L2} -> El producto de dos lenguajes L1 · L2 da como resultado un nuevo lenguaje que contiene la concatenación de cada una de las palabras x ∈ L1 con cada una de las palabras y ∈ L2
Por ejemplo:
L1 = {x ∈ {a,b}* : a ∈ Suf(x) }
L2 = {x ∈ {a,b}* : a ∈ Pref(x) }
L1 · L2 = {x ∈ {a,b}* : aa ∈ Seg(x) }
Al concatenar el lenguaje L1 (todas sus palabras terminan por a), con el lenguaje L2 (todas sus palabras comienzan por a), el resultado es un lenguaje que garantiza que la secuencia aa estará contenida en todas sus palabras.
Propiedades
1. (No conmutativa) -> L1 · L2 no necesariamente igual a L2 · L1
2. (Asociativa) -> (L1 · L2) · L3 = L1 · (L2 · L3)
3. (Elemento neutro) -> L · {λ} = {λ} · L = L
4. (Anulador) -> L · ∅ = ∅ · L = ∅
5. λ ∈ L1 · L2 ⇔ λ ∈ L1 ∧ λ ∈ L2
6. L1 · (L2 ∪ L3) = L1 · L2 ∪ L1 ·L3
Potencia
La potencia de un determinado lenguaje L elevado a un entero n>= 0 da como resultado un nuevo lenguaje que contiene la concatenación de cada una de sus palabras con todas las palabras de L, n veces. Es decir, debemos ir seleccionando cada palabra contenida en L y aplicarle la concatenación con cada una de las palabras de L.
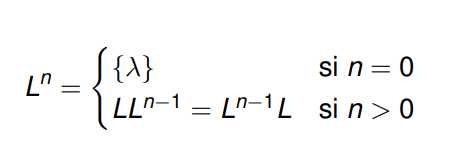
Por ejemplo, sea L = {aa, b}
L^2 = {bb, aab, baa, aaaa}, que es el resultado de aa·aa, aa·b, b·aa y b·b.
Propiedad
∅^0 = (Σ∗)^0 = {λ}^0 = {λ} -> Cualquier lenguaje elevado a 0 da como resultado la cadena vacía.
Clausura de Kleene sobre un Lenguaje
Aplicar la Clausura de Kleene sobre un determinado lenguaje L da como resultado un lenguaje infinito, aunque dicho lenguaje fuera finito inicialmente. Este nuevo lenguaje contendrá la unión de todas las potencias sobre L desde n = 0 hasta el infinito.

Es importante destacar que, la cadena vacía λ, únicamente podrá encontrarse en el lenguaje resultante si estaba inicialmente contenida en L, ya que al actuar de elemento neutro en la operación de concatenación, solo podrá estar presente si la concatenamos consigo misma.
Cociente

El cociente de un lenguaje, da como resultado un nuevo lenguaje que contendrá aquellas palabras que hayan sido «recortadas», ya sea por la izquierda o por la derecha. Por ejemplo, imaginemos que tenemos el siguiente lenguaje:
L = {x ∈ {a,b}* : a ∈ Pref(x) }
Si le aplicamos el cociente del símbolo a -> a^(-1)L, el lenguaje resultante será Σ*, pues el lenguaje L estaba compuesto por todas las palabras sobre el alfabeto Σ={a,b} que comienzan por a. Al haberle aplicado el cociente por la izquierda del símbolo a, hemos eliminado esta única restricción.
Lo mismo ocurre si definimos un lenguaje L2 = {x ∈ {a,b}* : a ∈ Suf(x) } y le aplicamos el cociente por la derecha del símbolo a. L2 a^(-1) = Σ*.
A tener en cuenta
Uno de los principales errores cuando se comienza a estudiar lenguajes formales, en la operación de cociente, es pensar que al realizar esta operación sobre un lenguaje L, el resultado incluye todas las palabras de L (eliminando los símbolos correspondientes en las palabras que se nos permita). Esto no es así, por ejemplo:
L= {recortar, revivir, hola, cartón, reparar, sol}
Si realizamos (re)^(-1)L el resultado incluye únicamente aquellas palabras sobre las que hemos podido aplicar el cociente.
En este caso (re)^(-1)L = {cortar, vivir, parar}.
Las palabras hola, cartón y sol no aparecen porque no es posible realizar (re)^(-1) sobre ellas.
Homomorfismo
Dados dos alfabetos Σ y Γ, un homomorfismo es una aplicación: h : Σ → Γ*
Esta definición puede extenderse a palabras:
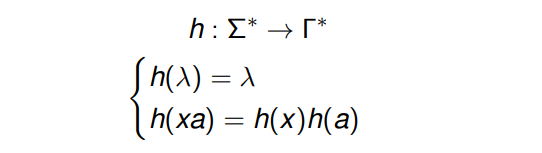
y a lenguajes: h(L) = {h (x) : x ∈ L}
En resumen, podemos ver un homomorfismo como un conjunto de «reglas» en el que asociamos cada símbolo de Σ con otro símbolo de Γ.
Por ejemplo, digamos que Σ = {a,b} Γ = {0,1} y que el homomorfismo viene dado por:
h(a) = 01
h{b} = λ
Esto quiere decir, que dada una palabra x, si aplicamos el homomorfismo sobre dicha palabra, cuando apareza un símbolo
a será sustituido por 01 y cuando aparezca un símbolo b será reemplazado por λ.
Ejemplo -> abbba = 0101, b = λ, ab = 01, bbba = 01, ababa = 010101
Si realizamos el homomorfismo sobre un lenguaje L, por ejemplo L = {x ∈ {a,b}* : a ∈ Pref(x) }
h(L) = {x ∈ {0,1}* : 01 ∈ Pref(x) } Ya que anteriormente todas las palabras debían comenzar estrictamente por a, al definir en la aplicación que el símbolo «a» corresponde a «01», todas las palabras de h(L) comenzarán por esta secuencia.
Homomorfismo inverso
Dado un homomorfismo h : Σ* → Γ*, se define el homomorfismo inverso como:
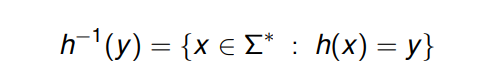
La operación puede extenderse para considerar lenguajes:
h^−1 (L) = {x ∈ Σ*: h(x) ∈ L}
Básicamente, cuando realizamos el homomorfismo inverso de un lenguaje, lo que estamos buscando es, dado un homomorfismo y un lenguaje L, encontrar qué anti-ímágenes de la aplicación pueden corresponder al lenguaje L al aplicar las reglas de h.
Por ejemplo, sea L1 = {x ∈ {a, b}*: aa ∉ Seg(x)} y h un homomorfismo que define las siguientes reglas:
h(0) = aa
h(1) = bab
h^−1 (L1) = {x ∈ {0, 1}* : |x|0 = 0} = {1}*
Dado que el lenguaje L2 contiene todas las palabras sobre {a,b}* que no tengan la secuencia «aa» en sus segmentos y el homomorfismo define que el símbolo «0» corresponde a la secuencia «aa», el homomorfismo inverso de L1 es un lenguaje sobre {0,1}* que contiene todas las palabras sin ceros, es decir 1*. En resumen, con esta operación, dado un lenguaje L y un conjunto de reglas u homomorfismo h, buscamos que palabras o lenguajes podrían darnos L como resultado al aplicar sobre ellas la aplicación del homomorfismo.
1. Lenguajes Formales
2. Autómatas Finitos
3. Regularidad de Lenguajes
Operaciones sobre Lenguajes
Una vez que hemos comprendido los conceptos de símbolo, alfabeto y palabra, y hemos explorado las operaciones que podemos realizar sobre estas últimas, es momento de introducir el concepto de lenguaje y las operaciones relacionadas con ellos.
A continuación, nos adentraremos en algunas de las operaciones principales sobre lenguajes dentro del campo de los lenguajes formales.
Definición de lenguaje
Un lenguaje L es un subconjunto de Σ* (la clausura de Kleene sobre un determinado alfabeto Sigma). Se incluyen:
∅ (lenguaje vacío, no contiene ninguna palabra)
Σ*(todas las palabras posibles sobre Σ)
Es importante matizar que los lenguajes son conjuntos de palabras sobre un determinado alfabeto. La naturaleza de conjunto de los lenguajes implica que se rigen por las propiedades de la Teoría de Conjuntos, tanto en notación como en las operaciones aplicables sobre ellos.
En la Teoría de Autómatas, los lenguajes juegan un papel fundamental, ya que los autómatas, como veremos en los próximos temas, son máquinas abstractas diseñadas para procesar entradas. Por lo tanto, al analizar un lenguaje dado, podemos determinar si es computable o no por un autómata.
Además, los lenguajes tienen una serie de propiedades que iremos desarrollando a lo largo de este curso. Por el momento solo nos concierne saber que estos pueden ser:
Finito: si tiene un número finito de palabras
Infinito numerable: podemos representarlo, pero contiene un número infinito de palabras
Notación de lenguajes
Dado que los lenguajes son conjuntos, la notación de estos mismos es muy similar. Para referirnos a un lenguaje
podemos hacerlo de dos formas. Digamos que Σ = {0,1} y Li una serie de lenguajes contenidos en Σ*.
Por extensión
Un conjunto se determina por extensión cuando se listan explícitamente los elementos del conjunto. Lógicamente, solo podremos referirnos a un lenguaje finito por extensión.
L1 = {λ,0,1,00,01,10,11} -> Lenguaje que contiene todas las palabras en Σ de longitud menor o igual a 2.
L2 = {000,001,010,011,100,101,110,111} -> Lenguaje que contiene todas las palabras de longitud 3 en Σ.
Por comprensión
Un conjunto se determina por comprensión, cuando se da una propiedad que cumplen todos los elementos del conjunto.
L1 = {x ∈ {0,1}* : |x| <= 2 } -> De esta forma citamos que L1 contiene todas las palabras x en la Clausura de Kleene sobre el alfabeto binario tal que su longitud es menor o igual a 2.
L2 = {x ∈ {0,1}* : |x| = 3 } -> Palabras de longitud 3.
L3 = {x ∈ {0,1}* : |x|0 MOD 2 = 0 } -> En este caso estamos inidcando que L3 contiene todas las palabras x en la Clausura de Kleene sobre el alfabeto binario tal que el número de ceros contenido en dichas palabras es par.
Es importante destacar que, a diferencia de los anteriores dos lenguajes L1 y L2, este lenguaje es infinito. Sin embargo, podemos especificar las propiedades que cumplen todas sus palabras. Así pues, dada una palabra cualquiera construida con ceros y/o unos seremos capaces de determinar si esta pertenece o no a L3.
Si tienes problemas para entender estos conceptos, en el siguiente vídeo tratamos las operaciones con conjuntos y su notación.
Una vez desarrollada la definición de lenguaje, veamos qué operaciones podemos realizar sobre estos.
Operaciones Booleanas
Como ya hemos explicado, los lenguajes son conjuntos formados por palabras. Esto significa que podemos realizar sobre ellos las operaciones booleanas definidas en conjuntos.
Unión
L1 U L2 = {x ∈ Σ∗: x ∈ L1 ∨ x ∈ L2} -> La unión de dos lenguajes da como resultado un nuevo lenguaje que contiene todas las palabras de cada uno de estos, comunes y no comunes (sin repetir). Por ejemplo:
L1 = {λ,0,1,00,01,10,11}
L2 = {000,001,010,011,100,101,110,111}
L1 U L2 = {λ,0,1,00,01,10,11,000,001,010,011,100,101,110,111}
Intersección:
L1 ∩ L2 = {x ∈ Σ* : x ∈ L1 ∧ x ∈ L2} -> La intersección de dos lenguajes da como resultado un nuevo lenguaje que contiene únicamente las palabras presentes en ambos, comunes (sin repetir). Por ejemplo:
L1 = {λ,0,1,00,01,10,11}
L2 = {000,001,010,011,100,101,110,111}
L1 U L2 = ∅ -> En este caso, al no tener palabras en común L1 y L2, su intersección da como resultado el conjunto vacío.
Propiedades Unión e Intersección
1.Asociativa
2.Conmutativa
3.Elemento neutro
- Unión: ∅ -> La unión de un lenguaje L con ∅ (el conjunto vacío) da como resultado el propio lenguaje L
- Intersección: Σ* -> La intersección de un lenguaje L con Σ* (todas las palabras posibles sobre un determinado alfabeto) da como resultado el propio lenguaje L.
4.Distributivas:
- L1 ∪ (L2 ∩ L3) = (L1 ∪ L2) ∩ (L1 ∪ L3)
- L1 ∩ (L2 ∪ L3) = (L1 ∩ L2) ∪ (L1 ∩ L3)
Complementación
Usualmente se representa con una línea en la parte superior del lenguaje, tal que así:

Sin embargo, también podemos encontrarla como una C en forma de exponente L^C -> complementario de C.
L^C = {x ∈ Σ*: x ∉ L} -> La complementación o complementario de un lenguaje L definido sobre un determinado alfabeto da como resultado un lenguaje que contiene todas las palabras que se pueden formar sobre dicho alfabeto y no se encuentran contenidas en L.
L1 = {x ∈ {0,1}* : |x| <= 2 }
L1^C = {x ∈ {0,1}* : |x| > 2 } -> El complementario de L1 es un lenguaje que contiene todas las palabras de longitud
mayor que dos.
Propiedades Complementación
1. Σ* = ∅
Por definición, la Clausura de Kleene recoge todas las palabras posibles sobre un alfabeto, de modo que su complementario no contiene ninguna palabra.
2. ∅^C = Σ*
3. (L^C)^C = L -> Si aplicamos dos veces la complementación a un lenguaje L, obtenemos el propio lenguaje L.
Operaciones definidas a partir de las booleanas
- Diferencia: L1 − L2 = L1 ∩ L2^C -> Palabras contenidas en L1 y no contenidas en L2
- Diferencia simétrica: L1 ⊖ L2 = (L1 ∩ L2^C) U (L1^C ∩ L2) -> Unión de palabras no comunes

Operaciones racionales: Producto
L1 · L2 = {xy ∈ Σ*: x ∈ L1 ∧ y ∈ L2} -> El producto de dos lenguajes L1 · L2 da como resultado un nuevo lenguaje que contiene la concatenación de cada una de las palabras x ∈ L1 con cada una de las palabras y ∈ L2
Por ejemplo:
L1 = {x ∈ {a,b}* : a ∈ Suf(x) }
L2 = {x ∈ {a,b}* : a ∈ Pref(x) }
L1 · L2 = {x ∈ {a,b}* : aa ∈ Seg(x) }
Al concatenar el lenguaje L1 (todas sus palabras terminan por a), con el lenguaje L2 (todas sus palabras comienzan por a), el resultado es un lenguaje que garantiza que la secuencia aa estará contenida en todas sus palabras.
Propiedades
1. (No conmutativa) -> L1 · L2 no necesariamente igual a L2 · L1
2. (Asociativa) -> (L1 · L2) · L3 = L1 · (L2 · L3)
3. (Elemento neutro) -> L · {λ} = {λ} · L = L
4. (Anulador) -> L · ∅ = ∅ · L = ∅
5. λ ∈ L1 · L2 ⇔ λ ∈ L1 ∧ λ ∈ L2
6. L1 · (L2 ∪ L3) = L1 · L2 ∪ L1 ·L3
Potencia
La potencia de un determinado lenguaje L elevado a un entero n>= 0 da como resultado un nuevo lenguaje que contiene la concatenación de cada una de sus palabras con todas las palabras de L, n veces. Es decir, debemos ir seleccionando cada palabra contenida en L y aplicarle la concatenación con cada una de las palabras de L.
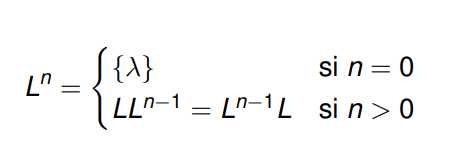
Por ejemplo, sea L = {aa, b}
L^2 = {bb, aab, baa, aaaa}, que es el resultado de aa·aa, aa·b, b·aa y b·b.
Propiedad
∅^0 = (Σ∗)^0 = {λ}^0 = {λ} -> Cualquier lenguaje elevado a 0 da como resultado la cadena vacía.
Clausura de Kleene sobre un Lenguaje
Aplicar la Clausura de Kleene sobre un determinado lenguaje L da como resultado un lenguaje infinito, aunque dicho lenguaje fuera finito inicialmente. Este nuevo lenguaje contendrá la unión de todas las potencias sobre L desde n = 0 hasta el infinito.

Es importante destacar que, la cadena vacía λ, únicamente podrá encontrarse en el lenguaje resultante si estaba inicialmente contenida en L, ya que al actuar de elemento neutro en la operación de concatenación, solo podrá estar presente si la concatenamos consigo misma.
Cociente

El cociente de un lenguaje, da como resultado un nuevo lenguaje que contendrá aquellas palabras que hayan sido «recortadas», ya sea por la izquierda o por la derecha. Por ejemplo, imaginemos que tenemos el siguiente lenguaje:
L = {x ∈ {a,b}* : a ∈ Pref(x) }
Si le aplicamos el cociente del símbolo a -> a^(-1)L, el lenguaje resultante será Σ*, pues el lenguaje L estaba compuesto por todas las palabras sobre el alfabeto Σ={a,b} que comienzan por a. Al haberle aplicado el cociente por la izquierda del símbolo a, hemos eliminado esta única restricción.
Lo mismo ocurre si definimos un lenguaje L2 = {x ∈ {a,b}* : a ∈ Suf(x) } y le aplicamos el cociente por la derecha del símbolo a. L2 a^(-1) = Σ*.
A tener en cuenta
Uno de los principales errores cuando se comienza a estudiar lenguajes formales, en la operación de cociente, es pensar que al realizar esta operación sobre un lenguaje L, el resultado incluye todas las palabras de L (eliminando los símbolos correspondientes en las palabras que se nos permita). Esto no es así, por ejemplo:
L= {recortar, revivir, hola, cartón, reparar, sol}
Si realizamos (re)^(-1)L el resultado incluye únicamente aquellas palabras sobre las que hemos podido aplicar el cociente.
En este caso (re)^(-1)L = {cortar, vivir, parar}.
Las palabras hola, cartón y sol no aparecen porque no es posible realizar (re)^(-1) sobre ellas.
Homomorfismo
Dados dos alfabetos Σ y Γ, un homomorfismo es una aplicación: h : Σ → Γ*
Esta definición puede extenderse a palabras:
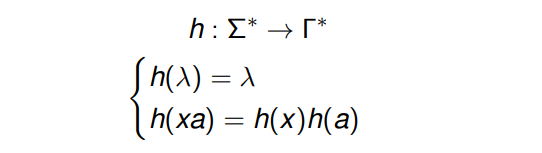
y a lenguajes: h(L) = {h (x) : x ∈ L}
En resumen, podemos ver un homomorfismo como un conjunto de «reglas» en el que asociamos cada símbolo de Σ con otro símbolo de Γ.
Por ejemplo, digamos que Σ = {a,b} Γ = {0,1} y que el homomorfismo viene dado por:
h(a) = 01
h{b} = λ
Esto quiere decir, que dada una palabra x, si aplicamos el homomorfismo sobre dicha palabra, cuando apareza un símbolo
a será sustituido por 01 y cuando aparezca un símbolo b será reemplazado por λ.
Ejemplo -> abbba = 0101, b = λ, ab = 01, bbba = 01, ababa = 010101
Si realizamos el homomorfismo sobre un lenguaje L, por ejemplo L = {x ∈ {a,b}* : a ∈ Pref(x) }
h(L) = {x ∈ {0,1}* : 01 ∈ Pref(x) } Ya que anteriormente todas las palabras debían comenzar estrictamente por a, al definir en la aplicación que el símbolo «a» corresponde a «01», todas las palabras de h(L) comenzarán por esta secuencia.
Homomorfismo inverso
Dado un homomorfismo h : Σ* → Γ*, se define el homomorfismo inverso como:
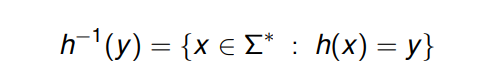
La operación puede extenderse para considerar lenguajes:
h^−1 (L) = {x ∈ Σ*: h(x) ∈ L}
Básicamente, cuando realizamos el homomorfismo inverso de un lenguaje, lo que estamos buscando es, dado un homomorfismo y un lenguaje L, encontrar qué anti-ímágenes de la aplicación pueden corresponder al lenguaje L al aplicar las reglas de h.
Por ejemplo, sea L1 = {x ∈ {a, b}*: aa ∉ Seg(x)} y h un homomorfismo que define las siguientes reglas:
h(0) = aa
h(1) = bab
h^−1 (L1) = {x ∈ {0, 1}* : |x|0 = 0} = {1}*
Dado que el lenguaje L2 contiene todas las palabras sobre {a,b}* que no tengan la secuencia «aa» en sus segmentos y el homomorfismo define que el símbolo «0» corresponde a la secuencia «aa», el homomorfismo inverso de L1 es un lenguaje sobre {0,1}* que contiene todas las palabras sin ceros, es decir 1*. En resumen, con esta operación, dado un lenguaje L y un conjunto de reglas u homomorfismo h, buscamos que palabras o lenguajes podrían darnos L como resultado al aplicar sobre ellas la aplicación del homomorfismo.
1. Lenguajes Formales
2. Autómatas Finitos
3. Regularidad de Lenguajes
Operaciones sobre Lenguajes
Una vez que hemos comprendido los conceptos de símbolo, alfabeto y palabra, y hemos explorado las operaciones que podemos realizar sobre estas últimas, es momento de introducir el concepto de lenguaje y las operaciones relacionadas con ellos.
A continuación, nos adentraremos en algunas de las operaciones principales sobre lenguajes dentro del campo de los lenguajes formales.
Definición de lenguaje
Un lenguaje L es un subconjunto de Σ* (la clausura de Kleene sobre un determinado alfabeto Sigma). Se incluyen:
∅ (lenguaje vacío, no contiene ninguna palabra)
Σ*(todas las palabras posibles sobre Σ)
Es importante matizar que los lenguajes son conjuntos de palabras sobre un determinado alfabeto. La naturaleza de conjunto de los lenguajes implica que se rigen por las propiedades de la Teoría de Conjuntos, tanto en notación como en las operaciones aplicables sobre ellos.
En la Teoría de Autómatas, los lenguajes juegan un papel fundamental, ya que los autómatas, como veremos en los próximos temas, son máquinas abstractas diseñadas para procesar entradas. Por lo tanto, al analizar un lenguaje dado, podemos determinar si es computable o no por un autómata.
Además, los lenguajes tienen una serie de propiedades que iremos desarrollando a lo largo de este curso. Por el momento solo nos concierne saber que estos pueden ser:
Finito: si tiene un número finito de palabras
Infinito numerable: podemos representarlo, pero contiene un número infinito de palabras
Notación de lenguajes
Dado que los lenguajes son conjuntos, la notación de estos mismos es muy similar. Para referirnos a un lenguaje
podemos hacerlo de dos formas. Digamos que Σ = {0,1} y Li una serie de lenguajes contenidos en Σ*.
Por extensión
Un conjunto se determina por extensión cuando se listan explícitamente los elementos del conjunto. Lógicamente, solo podremos referirnos a un lenguaje finito por extensión.
L1 = {λ,0,1,00,01,10,11} -> Lenguaje que contiene todas las palabras en Σ de longitud menor o igual a 2.
L2 = {000,001,010,011,100,101,110,111} -> Lenguaje que contiene todas las palabras de longitud 3 en Σ.
Por comprensión
Un conjunto se determina por comprensión, cuando se da una propiedad que cumplen todos los elementos del conjunto.
L1 = {x ∈ {0,1}* : |x| <= 2 } -> De esta forma citamos que L1 contiene todas las palabras x en la Clausura de Kleene sobre el alfabeto binario tal que su longitud es menor o igual a 2.
L2 = {x ∈ {0,1}* : |x| = 3 } -> Palabras de longitud 3.
L3 = {x ∈ {0,1}* : |x|0 MOD 2 = 0 } -> En este caso estamos inidcando que L3 contiene todas las palabras x en la Clausura de Kleene sobre el alfabeto binario tal que el número de ceros contenido en dichas palabras es par.
Es importante destacar que, a diferencia de los anteriores dos lenguajes L1 y L2, este lenguaje es infinito. Sin embargo, podemos especificar las propiedades que cumplen todas sus palabras. Así pues, dada una palabra cualquiera construida con ceros y/o unos seremos capaces de determinar si esta pertenece o no a L3.
Si tienes problemas para entender estos conceptos, en el siguiente vídeo tratamos las operaciones con conjuntos y su notación.
Una vez desarrollada la definición de lenguaje, veamos qué operaciones podemos realizar sobre estos.
Operaciones Booleanas
Como ya hemos explicado, los lenguajes son conjuntos formados por palabras. Esto significa que podemos realizar sobre ellos las operaciones booleanas definidas en conjuntos.
Unión
L1 U L2 = {x ∈ Σ∗: x ∈ L1 ∨ x ∈ L2} -> La unión de dos lenguajes da como resultado un nuevo lenguaje que contiene todas las palabras de cada uno de estos, comunes y no comunes (sin repetir). Por ejemplo:
L1 = {λ,0,1,00,01,10,11}
L2 = {000,001,010,011,100,101,110,111}
L1 U L2 = {λ,0,1,00,01,10,11,000,001,010,011,100,101,110,111}
Intersección:
L1 ∩ L2 = {x ∈ Σ* : x ∈ L1 ∧ x ∈ L2} -> La intersección de dos lenguajes da como resultado un nuevo lenguaje que contiene únicamente las palabras presentes en ambos, comunes (sin repetir). Por ejemplo:
L1 = {λ,0,1,00,01,10,11}
L2 = {000,001,010,011,100,101,110,111}
L1 U L2 = ∅ -> En este caso, al no tener palabras en común L1 y L2, su intersección da como resultado el conjunto vacío.
Propiedades Unión e Intersección
1.Asociativa
2.Conmutativa
3.Elemento neutro
- Unión: ∅ -> La unión de un lenguaje L con ∅ (el conjunto vacío) da como resultado el propio lenguaje L
- Intersección: Σ* -> La intersección de un lenguaje L con Σ* (todas las palabras posibles sobre un determinado alfabeto) da como resultado el propio lenguaje L.
4.Distributivas:
- L1 ∪ (L2 ∩ L3) = (L1 ∪ L2) ∩ (L1 ∪ L3)
- L1 ∩ (L2 ∪ L3) = (L1 ∩ L2) ∪ (L1 ∩ L3)
Complementación
Usualmente se representa con una línea en la parte superior del lenguaje, tal que así:

Sin embargo, también podemos encontrarla como una C en forma de exponente L^C -> complementario de C.
L^C = {x ∈ Σ*: x ∉ L} -> La complementación o complementario de un lenguaje L definido sobre un determinado alfabeto da como resultado un lenguaje que contiene todas las palabras que se pueden formar sobre dicho alfabeto y no se encuentran contenidas en L.
L1 = {x ∈ {0,1}* : |x| <= 2 }
L1^C = {x ∈ {0,1}* : |x| > 2 } -> El complementario de L1 es un lenguaje que contiene todas las palabras de longitud
mayor que dos.
Propiedades Complementación
1. Σ* = ∅
Por definición, la Clausura de Kleene recoge todas las palabras posibles sobre un alfabeto, de modo que su complementario no contiene ninguna palabra.
2. ∅^C = Σ*
3. (L^C)^C = L -> Si aplicamos dos veces la complementación a un lenguaje L, obtenemos el propio lenguaje L.
Operaciones definidas a partir de las booleanas
- Diferencia: L1 − L2 = L1 ∩ L2^C -> Palabras contenidas en L1 y no contenidas en L2
- Diferencia simétrica: L1 ⊖ L2 = (L1 ∩ L2^C) U (L1^C ∩ L2) -> Unión de palabras no comunes

Operaciones racionales: Producto
L1 · L2 = {xy ∈ Σ*: x ∈ L1 ∧ y ∈ L2} -> El producto de dos lenguajes L1 · L2 da como resultado un nuevo lenguaje que contiene la concatenación de cada una de las palabras x ∈ L1 con cada una de las palabras y ∈ L2
Por ejemplo:
L1 = {x ∈ {a,b}* : a ∈ Suf(x) }
L2 = {x ∈ {a,b}* : a ∈ Pref(x) }
L1 · L2 = {x ∈ {a,b}* : aa ∈ Seg(x) }
Al concatenar el lenguaje L1 (todas sus palabras terminan por a), con el lenguaje L2 (todas sus palabras comienzan por a), el resultado es un lenguaje que garantiza que la secuencia aa estará contenida en todas sus palabras.
Propiedades
1. (No conmutativa) -> L1 · L2 no necesariamente igual a L2 · L1
2. (Asociativa) -> (L1 · L2) · L3 = L1 · (L2 · L3)
3. (Elemento neutro) -> L · {λ} = {λ} · L = L
4. (Anulador) -> L · ∅ = ∅ · L = ∅
5. λ ∈ L1 · L2 ⇔ λ ∈ L1 ∧ λ ∈ L2
6. L1 · (L2 ∪ L3) = L1 · L2 ∪ L1 ·L3
Potencia
La potencia de un determinado lenguaje L elevado a un entero n>= 0 da como resultado un nuevo lenguaje que contiene la concatenación de cada una de sus palabras con todas las palabras de L, n veces. Es decir, debemos ir seleccionando cada palabra contenida en L y aplicarle la concatenación con cada una de las palabras de L.
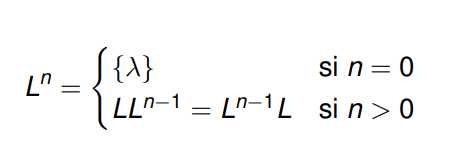
Por ejemplo, sea L = {aa, b}
L^2 = {bb, aab, baa, aaaa}, que es el resultado de aa·aa, aa·b, b·aa y b·b.
Propiedad
∅^0 = (Σ∗)^0 = {λ}^0 = {λ} -> Cualquier lenguaje elevado a 0 da como resultado la cadena vacía.
Clausura de Kleene sobre un Lenguaje
Aplicar la Clausura de Kleene sobre un determinado lenguaje L da como resultado un lenguaje infinito, aunque dicho lenguaje fuera finito inicialmente. Este nuevo lenguaje contendrá la unión de todas las potencias sobre L desde n = 0 hasta el infinito.

Es importante destacar que, la cadena vacía λ, únicamente podrá encontrarse en el lenguaje resultante si estaba inicialmente contenida en L, ya que al actuar de elemento neutro en la operación de concatenación, solo podrá estar presente si la concatenamos consigo misma.
Cociente

El cociente de un lenguaje, da como resultado un nuevo lenguaje que contendrá aquellas palabras que hayan sido «recortadas», ya sea por la izquierda o por la derecha. Por ejemplo, imaginemos que tenemos el siguiente lenguaje:
L = {x ∈ {a,b}* : a ∈ Pref(x) }
Si le aplicamos el cociente del símbolo a -> a^(-1)L, el lenguaje resultante será Σ*, pues el lenguaje L estaba compuesto por todas las palabras sobre el alfabeto Σ={a,b} que comienzan por a. Al haberle aplicado el cociente por la izquierda del símbolo a, hemos eliminado esta única restricción.
Lo mismo ocurre si definimos un lenguaje L2 = {x ∈ {a,b}* : a ∈ Suf(x) } y le aplicamos el cociente por la derecha del símbolo a. L2 a^(-1) = Σ*.
A tener en cuenta
Uno de los principales errores cuando se comienza a estudiar lenguajes formales, en la operación de cociente, es pensar que al realizar esta operación sobre un lenguaje L, el resultado incluye todas las palabras de L (eliminando los símbolos correspondientes en las palabras que se nos permita). Esto no es así, por ejemplo:
L= {recortar, revivir, hola, cartón, reparar, sol}
Si realizamos (re)^(-1)L el resultado incluye únicamente aquellas palabras sobre las que hemos podido aplicar el cociente.
En este caso (re)^(-1)L = {cortar, vivir, parar}.
Las palabras hola, cartón y sol no aparecen porque no es posible realizar (re)^(-1) sobre ellas.
Homomorfismo
Dados dos alfabetos Σ y Γ, un homomorfismo es una aplicación: h : Σ → Γ*
Esta definición puede extenderse a palabras:
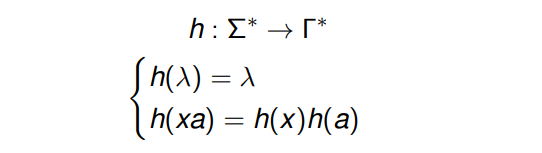
y a lenguajes: h(L) = {h (x) : x ∈ L}
En resumen, podemos ver un homomorfismo como un conjunto de «reglas» en el que asociamos cada símbolo de Σ con otro símbolo de Γ.
Por ejemplo, digamos que Σ = {a,b} Γ = {0,1} y que el homomorfismo viene dado por:
h(a) = 01
h{b} = λ
Esto quiere decir, que dada una palabra x, si aplicamos el homomorfismo sobre dicha palabra, cuando apareza un símbolo
a será sustituido por 01 y cuando aparezca un símbolo b será reemplazado por λ.
Ejemplo -> abbba = 0101, b = λ, ab = 01, bbba = 01, ababa = 010101
Si realizamos el homomorfismo sobre un lenguaje L, por ejemplo L = {x ∈ {a,b}* : a ∈ Pref(x) }
h(L) = {x ∈ {0,1}* : 01 ∈ Pref(x) } Ya que anteriormente todas las palabras debían comenzar estrictamente por a, al definir en la aplicación que el símbolo «a» corresponde a «01», todas las palabras de h(L) comenzarán por esta secuencia.
Homomorfismo inverso
Dado un homomorfismo h : Σ* → Γ*, se define el homomorfismo inverso como:
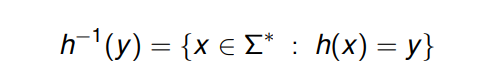
La operación puede extenderse para considerar lenguajes:
h^−1 (L) = {x ∈ Σ*: h(x) ∈ L}
Básicamente, cuando realizamos el homomorfismo inverso de un lenguaje, lo que estamos buscando es, dado un homomorfismo y un lenguaje L, encontrar qué anti-ímágenes de la aplicación pueden corresponder al lenguaje L al aplicar las reglas de h.
Por ejemplo, sea L1 = {x ∈ {a, b}*: aa ∉ Seg(x)} y h un homomorfismo que define las siguientes reglas:
h(0) = aa
h(1) = bab
h^−1 (L1) = {x ∈ {0, 1}* : |x|0 = 0} = {1}*
Dado que el lenguaje L2 contiene todas las palabras sobre {a,b}* que no tengan la secuencia «aa» en sus segmentos y el homomorfismo define que el símbolo «0» corresponde a la secuencia «aa», el homomorfismo inverso de L1 es un lenguaje sobre {0,1}* que contiene todas las palabras sin ceros, es decir 1*. En resumen, con esta operación, dado un lenguaje L y un conjunto de reglas u homomorfismo h, buscamos que palabras o lenguajes podrían darnos L como resultado al aplicar sobre ellas la aplicación del homomorfismo.
